page 4-2
適用版本:trueSpace4.0以上
發表日期:2000.3.15
正解
這個問題的重點在於︰「求出翻滾過程中,物體的軸心位置」。而因為物體是繞著一個定點
(應該說是繞著一個固定軸)
而翻滾,所以「軸心的行進路徑,正好是一個圓弧軌跡」。
提醒各位,如果你看到「要計算圓弧軌跡」,就要想到「極座標」公式,如下所示:
這個公式很簡單,也非常有用。在這個公式中,最重要的就是「半徑」(r)
以及「和座標軸的角度」(q)。
現在讓我們從「前視窗」來看正方體的翻滾過程,如圖3所示:
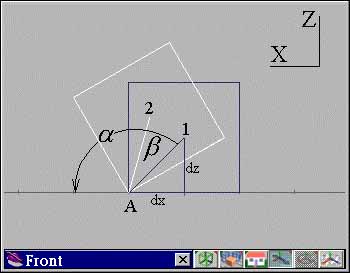 圖3 圖3
拿這個圖與「極座標公式」來探討,其中,「半徑」就是正方體的軸心
(點1) 到 A 點的距離,假設正方體的軸心座標為 (axes[0],axes[1],axes[2]),而假設
A 點的座標為 (origin[0],origin[1],origin[2]),因此半徑 (rad )
就是直角三角形的「斜邊」,寫成程式,就成為︰
dx = axes[0]-origin[0]
dz = axes[2]-origin[2]
rad = sqrt(pow(dx,2)+pow(dz,2))
# 求出半徑
|
現在再來看「角度」,一開始,正方體與 X 軸正向 (從前視圖來看的話,是左向)
的夾角是α(α=135),這個角度可以由底下的公式來算出︰
也就是說,α=atan(dz/dx),atan 是 tan 的反函數。
接著在翻滾的時候(翻滾一次是旋轉 90 度),正方體「逆時針」旋轉β角度
(旋轉是繞著 Y 軸,以前視窗來看,Y 軸是射向我們眼睛),因此角度就變成
α-β(點 2 到 X 軸的夾角)。
如此,我們可以從底下由極座標公式所寫成的程式碼,來計算正方體在翻滾過程中的軸心位置
(但角度要轉換為徑,因此要 *3.14159/180)︰
x1 = rad*cos((α-β)*3.14159/180)
z1 = rad*sin((α-β)*3.14159/180)
obj.Position = (x1,y1,z1)
# cube 是方塊物件
|
因為β可以由迴圈變數來控制而遞增,代表翻滾過程。最後,在每次翻滾一個角度位置後,也讓物體「繞著物件
Y 軸旋轉固定角度」,便算大功告成,也就是 obj.Rotate("y",deg)。
因此,我們就可以輕鬆完成下一頁的程式內容 (只有 34 行),而讓正方體連續翻滾。
|
 圖3
圖3