page 4-3
適用版本:trueSpace4.0以上
發表日期:2000.3.15
- 您可以trueSpace4中加入一個正方體,並開啟程式編輯器,將下面的程式複製到程式編輯器中,如圖4。
- 按下Python Script編輯器中的開始播放,您就可以看到程式進行運算,同時正方體也跟著翻滾,此時正在進行動畫的記錄。
- 完成後在trueSpace4中按下動畫播放,就可以看到剛才所記錄的動畫。
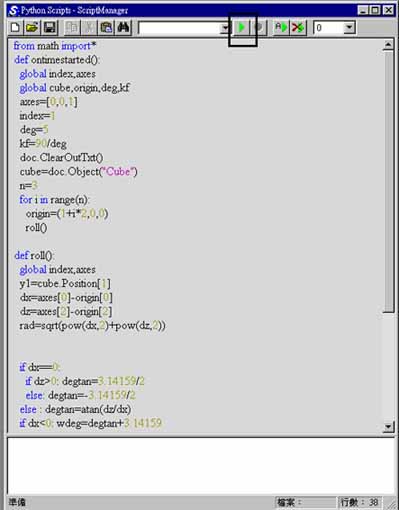 圖4 圖4
詳細的程式如下:
from math import*
def ontimestarted():
global index,axes
global cube,origin,deg,kf
axes=[0,0,1] # 軸心
index=1 # 動畫從第 1 格開始 (可從任何格開始)
deg=5 # 每次旋轉 5 度
kf=90/deg # 所以有 18 個關鍵畫面
doc.ClearOutTxt()
cube=doc.Object("Cube")
n=3 # 翻滾 3 次,共 54 格(如果你要翻滾多次,只要修改數值即可)
for i in range(n):
origin=(1+i*2,0,0) # A,B,C 三點
roll()
def roll():
global index,axes
y1=cube.Position[1] # Y 座標位置不變
dx=axes[0]-origin[0]
dz=axes[2]-origin[2]
rad=sqrt(pow(dx,2)+pow(dz,2)) # 計算半徑
# 底下的程式碼,是要求出角度
a (即 wdeg)
if dx==0:
if dz>0: degtan=3.14159/2
else: degtan=-3.14159/2
else : degtan=atan(dz/dx)
if dx<0: wdeg=degtan+3.14159
else: wdeg=degtan
# 計算翻滾過程中的物體軸心位置(β=deg*k)
for k in range(1,kf+1):
doc.ActiveTime=index
cube.Rotate("y",deg)
x1=rad*cos(wdeg-(deg*k)*3.14159/180)+origin[0]
z1=rad*sin(wdeg-(deg*k)*3.14159/180)+origin[2]
cube.Position=(x1,y1,z1)
index=index+1
# 修正翻滾後的軸心
axes[0]=-dx+origin[0] |
|